That time I saw a weird rainbow

A single primary bow can be seen when sunlight rays are refracted once inside raindrops, split into different wavelengths (colours) and travel towards the observer standing between the Sun and the rainbow. Rays exit the droplet at an angle of 42 degrees downwards relative to the original sunlight direction, as depicted below (Source: Wikipedia Commons)

Single rainbows are awesome on their own, but sometimes they're accompained by additional concentric bows:

• A secondary bow can appear around the primary one, caused by a second refraction of sunlight inside rain droplets. The secondary bow is concentric to primary one, appears approximately 10 degrees outside, is significantly fainter and its colors are reversed. Primary + secondary form the relatively common "double rainbow" that everybody loves. More details here.
• Supernumerary bows can appear adjacent to the inside of any bow and seem to repeat the same color pattern, but compressed. They are caused by lightwave interference, which is awesome, but we won't dig any deeper for now. More detals here.

The picture below shows a faint secondary bow above the primary one, and part of a supernumerary right below the primary violet shade.

These are very cool, but definitely not what I saw.

Reflection rainbows are formed by two separate bows: a primary one caused by direct sunlight, and a reflection one above the primary, caused by sunlight reflected on a water surface that must be behind the observer, and calm enough for sunlight to reflect in a coherent direction instead of scattering. The reflection bow is not concentric, and appears above the primary one. More details here.

Twinned rainbows are very rare, and apparently not yet fully understood. A possible explanation is that they're primary bows that bifurcate in some sections due to the presence of larger droplets that become non-spherical under the effect of air friction, and refract light in a slightly different direction, so the rays that reach the observer come from slightly above/below the primary bow. More details here.

The picture below shows a twinned primary bow and secondary bow above it (Source: Wikimedia Commons)

I was lucky to find the SunCalc site, and used it to generate a map of the area that includes the Sun configuration relative to the camera position at the time of observation (21/05/2019 21:00).

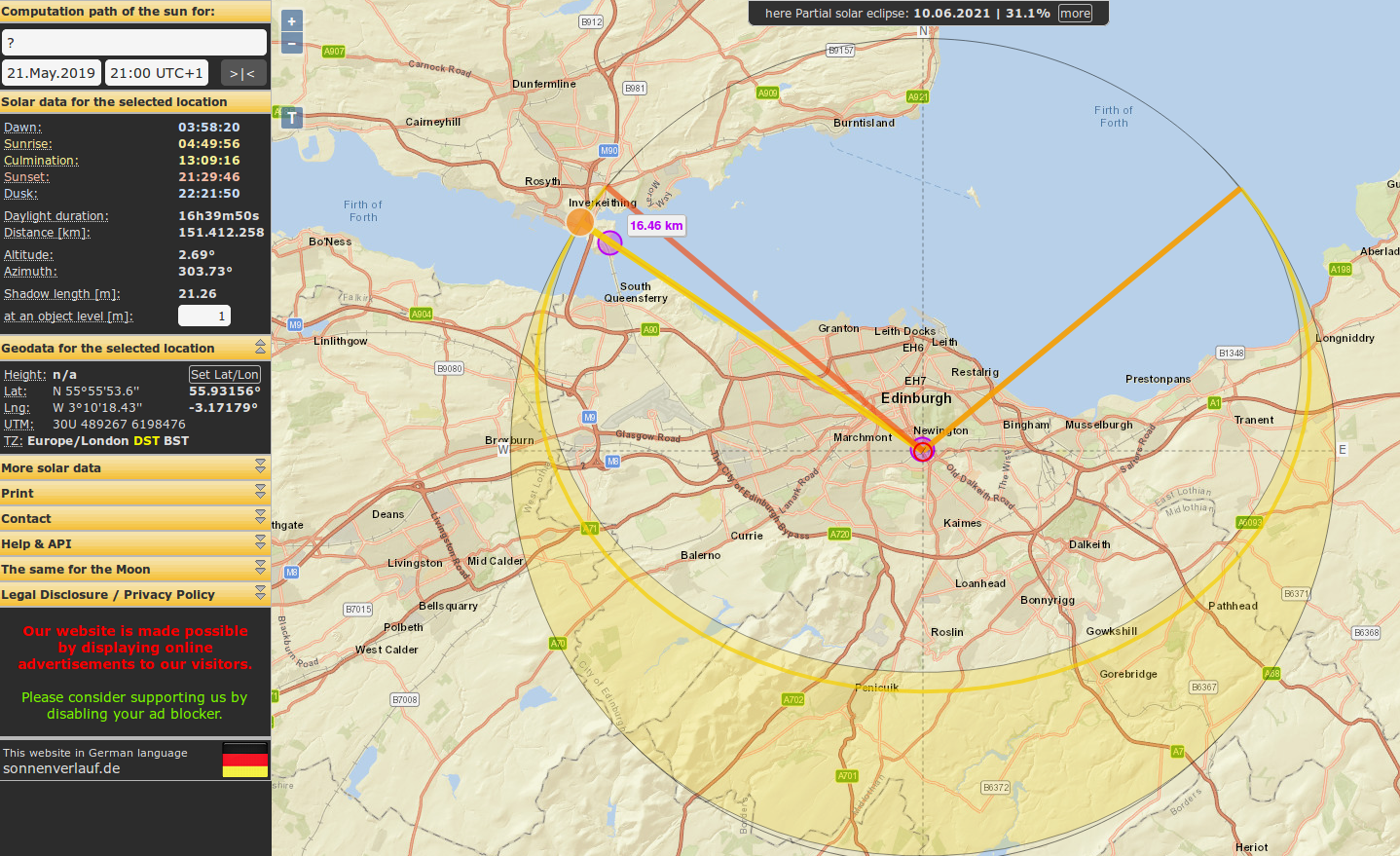
This image answers question 1, and provides data that will help answer question 2:

• The Sun direction matched the observed rainbow orientation, with a and altitude of \(2.7\) degrees above the horizon.
• There was a large water body that extends from \([10\text{km},16.5\text{km}]\) behind the camera, the Firth of Forth.

Assuming a perfect mirror water surface, we can infer that if the Sun rays that caused the primary bow hit the raindrops with an angle of \({\color[RGB]{247,189,0} \alpha_p} = -2.7\) deg, then their specular reflection on the water that caused the reflection bow hit the rain droplets at an angle of \({\color[RGB]{0,126,225} \alpha_r} = +2.7\) deg.

I needed the apex heights of the primary and reflection bows, but they were incomplete, so I manually reconstructed the full bows from the partial picture, by mirroring it horizontally and matching a circle to each bow using Inkscape. This is obviously an approximation, but the conclusion seems to prove it was good enough, so hooray for scrappy Science.

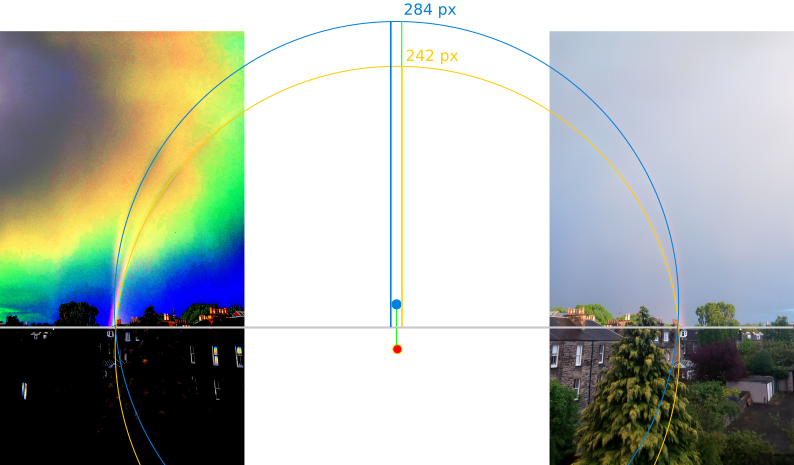
From this picture I computed the heights in pixels: \({\color[RGB]{247,189,0} y_p} = 242\) px (primary) and \({\color[RGB]{0,126,225} y_r} = 284\) px (reflection). I did not count the pixels one by one, I promise.

The diagram below shows primary bow data in orange and reflection bow data in blue. Reflection triangle angles are \(A=2.7\), \(B=135.3\), \(C=42\).

The next diagram zooms on the observer-horizon-bow triangles on the right of the observer (origin). View angles above the horizon are \({\color[RGB]{247,189,0} \theta_p} = 39.3\) and \({\color[RGB]{0,126,225} \theta_r} = 44.7\), computed from the known light-eye droplet reflection angle \(42\) and the Sun and reflection elevations \({\color[RGB]{247,189,0} \alpha_p} = -2.7\) and \({\color[RGB]{0,126,225} \alpha_r} =2.7\).

Observer distances along the horizon (x-axis) to the primary and reflection bows are unknown, but assumed to be equal \({\color[RGB]{247,189,0} x_p} = {\color[RGB]{0,126,225} x_r} = x\), as they were most likely caused by the same curtain of raindrops.

Assuming bow apex heights in the picture are perpendicular to the horizon (y-axis), we have 2 rectangle triangles

\begin{eqnarray*} \tan( {\color[RGB]{0,126,225} \theta_r} ) = {\color[RGB]{0,126,225} y_r} / x \\ \tan( {\color[RGB]{247,189,0} \theta_p} ) = {\color[RGB]{247,189,0} y_p} / x \end{eqnarray*}

we can get rid of the unknown \(x\) easily by dividing the 2 equations

\[\frac{\tan( {\color[RGB]{0,126,225} \theta_r} )}{\tan( {\color[RGB]{247,189,0} \theta_p} )} = \frac{ {\color[RGB]{0,126,225} y_r} }{ {\color[RGB]{247,189,0} y_p} }\]

and operating we arrive at \(1.209 \approx 1.173\) with a relative error of \(3\%\) or an accuracy of \(97\%\), not too bad!

We have our answer, but it's slightly unsatisfying. In particular, we used known angles, but we did not need to consider the distance to the water at all… Maybe we can use it to validate or disprove the conclusion?

One idea is to compute how high is the rainbow? and verify the answer is reasonable. Clouds at Edinburgh's latitude extend between roughly 500m to 10km above the sea (details later). If we compute the height and it's significantly outside that range we'd need to reconsider.

From the reconstructed picture we know the bow heights in pixels, but not in meters. It turns out that with the data we have it's easier to first compute the observer distance to the rainbow \({\color[RGB]{0,126,225} d_r}\) rather than its height \({\color[RGB]{0,126,225} y_r}\) over the horizon… This is worth mentioning because, in general, the distance to a single primary bow cannot be known: it could be anywhere along the viewing direction, and we have no additional data required to triangulate its height (details here).

Fortunately, we know the distance range to the water reflection that causes the reflection bow \(c=[10,16.5]\text{km}\), so we can compute its height \({\color[RGB]{0,126,225} y_r}\) as follows.

Using the law of sines \[ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} \]

we isolate \({\color[RGB]{0,126,225} d_r} = a\) and obtain a distance range \[ {\color[RGB]{0,126,225} d_r} = c \frac{\sin(A)}{\sin(C)} = [10,16.5] \times 0.0704 = [0.7,1.16] \text{km} \]

and using \({\color[RGB]{0,126,225} d_r}\) and the view angle \({\color[RGB]{0,126,225} \theta_r}\) we obtain a height range

\[ {\color[RGB]{0,126,225} y_r} = {\color[RGB]{0,126,225} d_r}\sin({\color[RGB]{0,126,225} \theta_r}) = [0.7,1.16] \times 0.703 = [0.492,0.816] \text{km} \]

This range between roughly 500m to 800m is within the expected values for low clouds, from 500m to 3km (details). The clouds in the picture did look pretty low indeed, as usual in Edinburgh, so I'm finally convinced: I saw a reflection rainbow, and my lost keys were under the streetlight.